La enseñanza burocrática sigue las exigencias del estado, pero no los principios de una buena pedagogía.
En la actualidad, los profesores ya no son educadores. Son funcionarios del gobierno que tienen que implementar las políticas del gobierno en el aula. Y aun si han entendido lo que es una buena pedagogía – no pueden aplicarla, porque las exigencias del currículo estatal tienen que cumplirse primero.
Aquí en el Perú por lo menos, este currículo no toma en cuenta ni lo que se sabe acerca del desarrollo del niño, ni los principios didácticos más elementales – especialmente para las matemáticas. En particular deseo resaltar los siguientes puntos:
– Según el desarrollo cerebral del niño promedio, la enseñanza escolar formal no es provechosa antes de los 8 a 10 años de edad. Estos niños están recién entrando a la etapa de las operaciones concretas, y por tanto las operaciones matemáticas todavía no les parecen lógicas, ni pueden formarse un concepto de ellas en su mente. (Vea más detalles sobre esto en «Mejor tarde que temprano».) Por tanto, antes de esta edad, la enseñanza de la matemática debería centrarse en los principios fundamentales y en las operaciones básicas con números pequeños, de tal manera que el alumno puede reproducirlos manipulando objetos concretos. Lo que va más allá de esto, a una edad temprana, les hace más daño que bien a los niños.
– Cada niño tiene su propio ritmo de desarrollo y debe ser enseñado según el estado de desarrollo que alcanzó, no según su edad cronológica. Si intentamos hacer caminar a la fuerza a un bebé de tres meses, le hacemos daño. De la misma manera le hacemos daño a un niño cuando lo forzamos a resolver tareas que según su estado de desarrollo no puede entender todavía.
(Siempre se podrá encontrar a uno u otro niño precoz que llega a entender operaciones abstractas a una edad temprana. Pero estas son excepciones y no deben tomarse como norma para un sistema escolar generalizado. A estos niños precoces se les debería permitir saltar grados escolares o recibir cursos especiales según sus intereses, pero sin obligar a los otros niños a seguir el paso acelerado de ellos.)
– Cada nuevo conocimiento debe basarse sobre un conocimiento previo con el cual el niño ya está familiarizado. Esto es de particular importancia para la matemática, porque cada principio más avanzado se basa sobre una multitud de otros principios más sencillos. Por tanto, es necesario que el niño entienda bien los principios sencillos, antes de enseñarle principios más difíciles. (Por ejemplo, un niño no puede entender las potencias si no ha entendido primero la suma y después la multiplicación.)
– Cantidad no es calidad. Cuánto más conocimientos un niño tiene que absorber en un tiempo dado, tanto más es la cantidad de conocimientos anteriores que olvida. Por tanto, aumentar las horas académicas y acelerar el paso no hace que los niños aprendan más. Al contrario, cuando se sobrepasa cierto límite, los niños olvidan más de lo que aprenden. Una buena pedagogía le da al niño el tiempo que necesita para asimilar un nuevo conocimiento, y lo profundiza hasta que el niño esté seguro en ello. Y una buena pedagogía mantiene un equilibrio sano entre estudio intelectual, actividad física, trabajo manual, juego y descanso.
En completa contradicción contra todos estos principios, dice el Proyecto Educativo Nacional (PEN) del Perú:
«Prevenir la deserción y la repetición en la educación primaria
La repetición de grado agrava la extraedad -superación de la edad normada para el grado- desalentando a los niños e incrementando el riesgo de fracaso o abandono. Pero la promoción de grado con bajo rendimiento acumula el déficit y habitúa a la mediocridad. Las escuelas no tienen mecanismos que prevengan estas situaciones o las corrijan con rapidez, dejando a cada niño librado a su suerte. Esta política busca disminuir y suprimir los índices de abandono y repetición escolar, en especial en zonas urbanas y rurales con mayor riesgo de fracaso, mediante la creación de sistemas de apoyo y acompañamiento educativo.
PRINCIPALES MEDIDAS
a) Sistemas de detección oportuna de niños y niñas en riesgo de repetición y abandono escolar, bajo la responsabilidad de los docentes en cada grado y sección.
b) Institucionalización de estrategias pedagógicas diferenciadas de recuperación, atención educativa y tutoría a estudiantes en riesgo de repetir y abandonar el año, que incluya el empleo de horas adicionales.
(…)»
(Proyecto Educativo Nacional al 2021, Ministerio de Educación del Perú, 2007)
Esto significa, hablando claramente: Todos los niños son forzados a comenzar la escuela primaria a los seis (o cinco) años y terminarla a los once años, sin considerar su desarrollo individual. Un niño que no alcanza las metas del año, es obligado a pasar horas extra en la escuela hasta ya no poder más, porque obligatoriamente tiene que pasar de grado a la «edad normada», dictada por la burocracia. (La situación actual es que gracias a esta política, muchos niños ya no tienen fines de semana libres ni vacaciones.) El Ministerio de Educación no considera el hecho de que algunos niños se desarrollan más tarde que otros, ni el hecho de que el exceso de horas académicas les hace un daño serio. En vez de dejar que los niños sean niños, son obligados a convertirse en «calculadoras humanas», a una edad en la que deberían disfrutar del calor de un hogar y jugar sin preocupaciones. La mayoría de los niños no pueden cumplir con estas exigencias que se les imponen de manera burocrática, sin ninguna consideración pedagógica. Esta es una situatión muy trágica: Estos mismos niños podrían rendir muy bien, y con mucho menos horas académicas y mucho menos sufrimiento, si tan solamente les fuera permitido ser niños por dos o tres años más. Existen cientas de evidencias para ello, de investigaciones realizadas alrededor del mundo entero. El Dr.Raymond Moore recopiló muchas de ellas en su libro «Mejor tarde que temprano». Pero los planificadores de la educación simplemente no toman en cuenta lo que es lo mejor para los niños.
Aun los mejores profesores tienen que fracasar con una tal política, porque no se les permite enseñar a los niños de acuerdo a su propio desarrollo. Niños de cinco, seis, siete años están siendo sofocados bajo una tal avalancha de conocimientos y tareas que nunca pueden asimilarla. No les queda otra salida que «aparentar» y «adivinar». Para cuando llegan a cuarto o quinto grado, la mayoría ya está completamente desconectada de los conocimientos matemáticos que se exigen de ellos. Su «matemática» es un castillo en el aire sin fundamento, porque se les exige entender fracciones, potencias y raíces, cuando todavía no han asimilado ni los principios fundamentales de la suma, resta y multiplicación. Por ejemplo, son muy, muy escasos los alumnos de primaria que son capaces de solucionar correctamente un problema como este:
«Un cocodrilo mide 3,50 m (con cola). Su cuerpo mide un metro más que su cola. ¿Cuánto mide la cola del cocodrilo?»
Sin embargo, este problema no requiere nada más que las operaciones básicas, y un poco de razonamiento lógico. Pero los mismos niños que todavía no pueden entender esto, tienen que aprender a calcular con decimales y a sacar raíces cuadradas. Puesto que no tienen fundamento, todo esto no hace sentido para ellos, y tan pronto como lo aprenden, lo vuelven a olvidar. Entran a la escuela secundaria sin siquiera haber tenido tiempo para aprender bien la tabla de multiplicación; y en la secundaria tienen que volver a aprender lo que ya se les enseñó en la primaria. (Esto no es ningún chiste. Un día tuve en la mañana una alumna de refuerzo que estaba en tercer grado de primaria, y en la tarde otra que estaba en tercero de secundaria. Sus tareas que habían recibido en la escuela, eran casi idénticas.)
Tanto profesores como alumnos están bajo tal presión de «alcanzar las metas educativas» (ilusorias), que tienen que cubrir una multitud de temas, pero no tienen tiempo para aprender bien ninguno de ellos. Entonces los alumnos lo olvidan, y en el año siguiente tienen que volver a aprender lo mismo de nuevo.
Mencionaré solamente dos temas matemáticos que los alumnos están obligados a aprender mucho antes de que puedan realmente comprenderlos:
– Sumar llevando y restar prestando, con números de tres cifras. Esto se enseña ahora en primer grado, cuando muchos todavía no saben ni sumar números menores de 10. Como procedimiento mecánico, un niño de esta edad puede hacerlo – pero de ninguna manera entiende lo que hace. Para poder entenderlo, tendría que entender cómo funciona el sistema decimal – y esto a su vez presupone entender la multiplicación. Además tendría que ser capaz de relacionar un número de tres cifras con un concepto concreto; pero la imaginación de un niño de esta edad todavía no puede distinguir entre «cincuenta» y «quinientos».
– Fracciones. Imaginarse algo más pequeño que una unidad, es algo muy difícil para un niño de ocho años (a esta edad se enseñan actualmente las fracciones). Se le puede mostrar un círculo dividido en partes, y el niño puede contar las partes; pero si tiene muchas partes, entonces ¿cómo pueden todas estas partes juntas ser «1»? Esta es una paradoja irresoluble para la mayoría de los niños de esta edad. – Por supuesto, las fracciones presuponen entender las leyes de la multiplicación y división. Y no solo esto: simplificar, sumar y restar fracciones se basa sobre los conceptos del máximo común divisor (MCD) y mínimo común múltiplo (MCM). Esto a su vez presupone el concepto de múltiplos, divisores, números compuestos y números primos, y factores primos. Todo esto debería enseñarse antes – y no solo enseñar; habría que asegurarse de que los niños lo entiendan. Y habría que relacionar estos conceptos al nivel de principios. Pero la enseñanza burocrática exige que los niños calculen con fracciones sin tener nada de este fundamento. No es de extrañar que los alumnos no entiendan nada.
La enseñanza burocrática es incapaz ante los desafíos de la vida real y del sentido común.
| Quedémonos un poco más con las fracciones. Los alumnos aprenden un procedimiento que llaman «CC» o «C doble» para tratar con fracciones dobles: |
 |
Mientras este procedimiento rinde el resultado correcto, no enseña nada acerca de los principios que rigen las fracciones. Los alumnos saben aplicarlo mecánicamente, pero se quedan perplejos ante expresiones como las siguientes:
En el caso a), a algunos todavía se les ocurre que 3 es igual a tres enteros, entonces lo escriben así y aplican su acostumbrada «CC» (aunque es un exceso innecesario de trabajo):

Pero el caso b) ya no permite esto. La enseñanza burocrática no puede preparar al alumno para una situación como esta, porque tendría que prescribir un nuevo procedimiento para cada caso especial que se podría presentar.
Pero un alumno que ha aprendido los principios de la matemática, no tendrá muchos problemas aquí. Para él, los mismos principios que rigen una fracción doble, se pueden aplicar también a una fracción triple, cuadruple o más complicada. Primeramente, para este alumno será claro como el agua que una fracción es solamente otra forma de escribir una división. Entonces, la expresión b) es equivalente a: 4 : 3 : (5 : ((7 : 8) : 11)). Y este alumno entenderá también qué efecto tiene un signo de división : ante un paréntesis. (Incluso entenderá que estos principos son equivalentes a las leyes de signos en la suma y resta.) Aplicando estos principios, y un poco de sentido común, resolverá el problema de la misma manera como resolvería una fracción doble – sabiendo lo que hace.
Pero «sentido común» es incompatible con «burocracia». El sencillo problema del cocodrilo, que cité más arriba, se puede resolver con un poco de sentido común y con muy poco de matemáticas (incluso sin recurrir a una ecuación). La mayoría de los alumnos actuales no pueden resolverlo porque la burocracia no cultiva el sentido común. Los problemas que exigen sentido común son el mayor desafío a la burocracia: no existe ningún procedimiento reglamentario para resolverlos.
Este es otro ejemplo, de la vida diaria y ordinaria:
«Mamá compró papas por S/.1.80, un queso por seis soles, y un coliflor. Pagó con un billete de diez soles y recibió 60 centavos de vuelto. ¿Cuánto costó el coliflor?»
Ante un problema como este, la mayoría de los niños (aun en sexto grado) no saben si deben sumar, restar, multiplicar o dividir. Esto indica ¡que todavía no comprendieron ni aun los principios de la suma y resta! – Cierto, saben sumar y restar mecánicamente números de siete y más cifras. Pero esto todavía no es «comprender» la suma y la resta. Estos conceptos son «comprendidos» solamente cuando el alumno es capaz de relacionarlos con los sucesos de la vida diaria. Pero esto es algo que la escuela no les puede enseñar, porque la escuela es burocrática y por tanto es desconectada de la vida real y del sentido común.
Una muy buena alumna en matemática que conocí, pasaba muchas horas ayudando a sus padres en atender su negocio. Esta fue la mejor preparación en matemática que podía recibir. Se acostumbraba a calcular los precios y dar el cambio correcto, y a pagar facturas correctamente. Esto es aplicar principios en la vida diaria, y esto le ayudó más que cualquier enseñanza que podía recibir en la escuela.
La enseñanza burocrática tiene que capitular ante esta clase de problemas. Algunos profesores se esfuerzan por sistematizarlos y mecanizarlos y proveer alguna «pauta de burro» a sus alumnos: «Si son varias compras juntas, hay que sumar. Si es dar cambio, hay que restar. Si son tres de la misma cosa, hay que multiplicar por tres …» – Estos son esfuerzos vanos. La vida real no se deja mecanizar de esta forma; siempre aparecerá un caso que no encaja en ninguna de las categorías preformuladas por el profesor. Pero la vida real puede comprenderse a base de principios. Y el que ha comprendido los principios, ya no necesita las «pautas de burro».
Rebeca Wild explica ante el trasfondo de las investigaciones de Jean Piaget, como se destruye el verdadero aprendizaje cuando la enseñanza consiste en tales memorizaciones de reglas. Dice acerca de la «etapa de las operaciones concretas» (que dura en la mayoría de los niños aproximadamente desde los siete u ocho años hasta los trece a quince años de edad):
«La comprensión solo está asegurada si el niño tiene los objetos en la mano o si los conoce muy bien de experiencias anteriores. … Si en esta etapa … se intenta utilizar símbolos, por mucho que se los haya simplificado, el niño se ve obligado a tomar una especie de medida de defensa: tendrá que utilizar su memoria para poder repetir, cuando se lo pidan, el saber requerido. (…) Claparède formuló la siguiente ley: todo lo que en su día fue aprendido de memoria, más tarde es mucho más difícil de entender. No es extraño que observemos con tanta frecuencia lo mucho que esta práctica del aprender reglas dificulta una aplicación inteligente.»
(Rebeca Wild, «Educar para ser», Barcelona 1999)
(Para los curiosos: La aplicación correcta de suma y resta es concisamente resumida en este axioma, formulado asi por Euclides: «El entero es más grande que su parte.» El que ha comprendido esto (¡no digo «memorizado»!), ya no tendrá el problema de si debe sumar o restar. Pero hallé que es asombrosamente difícil para alumnos educados en un sistema burocrático, comprender un axioma tan sencillo como este.)
Entre los problemas un poco más «escolares», unos que también desafían la enseñanza burocrática son los criptogramas. Es imposible prescribir un procedimiento mecanizado para la solución de criptogramas. Cada criptograma se basa en una propiedad distinta que debe ser descubierta – a base de principios. Por eso, los criptogramas están entre los ejercicios más excelentes para entrenar la capacidad de razonar. Pero encuentro que justo este tipo de ejercicios es omitido por casi todos los cursos de (mal llamado) «razonamiento matemático». Estos cursos, por lo general, se limitan a tareas que se pueden mecanizar más fácilmente, tales como el conteo de segmentos y figuras, continuar secuencias, etc.
.
Algunos procedimientos de la enseñanza burocrática son incluso contrarios a los principios matemáticos.
A la burocracia no le interesa si se respetan los principios o no. Sus procedimientos deben llevarse a cabo, aun si guían al alumno por un camino falso. Mencionaré dos procedimientos con los que me encuentro casi diariamente, que efectivamente hacen que los alumnos aprendan principios equivocados. El procedimiento en sí rinde el resultado correcto – pero lo alcanza por un camino que enseña algo equivocado:
1. Poner el signo al lado equivocado.
En la mayoría de los libros de matemática para primaria, encuentro restas verticales escritas así: |
 |
Esto da la impresión de que el signo «menos» (-) estaría asociado con el número 345. Pero el número que se resta es 238 y no 345. Hablando en sentido vectorial, 345 es el número que tiene dirección positiva, y 238 es el número que tiene dirección negativa. Por tanto, el signo «-» debe estar delante de 238 y no detrás de 345.
Esto puede parecer un detalle sin mayor significado, pero no lo es. En realidad, este error «insignificante» les causa a los alumnos un dolor de cabeza que perseguirá a algunos hasta el fin de su educación secundaria. Es que más adelante tendrán que reducir expresiones algebraicas como esta:
3a + 5b – 7 + 4b – 6a
Muchos alumnos, (mal) acostumbrados durante años a escribir el signo «-» a la derecha del número, asocian instintivamente en su mente las expresiones así:
Entonces agruparán la expresión de una de las siguientes formas, que son ambas equivocadas:
| 3a + |
6a +? (-?) |
5b – |
4b – |
7 |
A diferencia de los casos que mencioné anteriormente, poner el signo al lado correcto no es una exigencia burocrática sin sentido. Es una cuestión de principios que afecta el aprendizaje de las leyes de la matemática. Pero a la burocracia no le interesa si se aprenden principios correctos o equivocados o ningún principio. Por eso, este error parece no molestar a nadie.
| En sí, poner el signo al lado derecho o izquierdo no es ningún principio; es una convención. O sea, es un acuerdo mutuo entre los matemáticos. Podríamos cambiar la convención y ponernos de acuerdo en que desde aquí en adelante pondremos el signo a la derecha del número. Pero entonces, la resta citada al inicio tendría que escribirse así (vea a la derecha): |
 |
En este ejemplo, ningún principio de la matemática nos permite asociar el signo negativo con el número 345, sea a la derecha o a la izquierda. Es simplemente un error, y uno que tiene consecuencias, como vimos arriba. No por cuestiones burocráticas, sino por una cuestión de principios.
2. «Llevar algo al otro lado» en una ecuación.
Aquí tenemos una ecuación sencilla. A veces pido a un alumno que me explique cómo resolverla:
x + 5 = 18
Casi siempre recibo la siguiente explicación: «Llevo el 5 al otro lado y le cambio el signo.» – Esta explicación es técnicamente correcta, pero contradice completamente los principios matemáticos.
El principio general de las ecuaciones es el principio de la igualdad. La mejor ilustración visual de una ecuación es la imagen de una balanza en equilibrio:
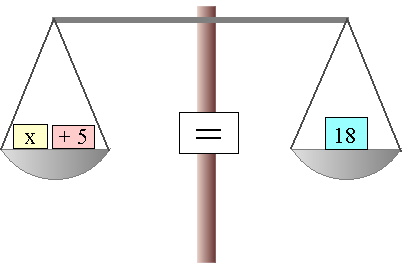
Para resolver una ecuación, es necesario mantener este equilibro durante el proceso entero. Solamente así puedo asegurar que al final, cuando tengamos despejada la incógnita «x», el signo de igualdad «=» siga siendo verdadero.
Ahora, si «llevo algo al otro lado», la balanza obviamente ya no está en equilibrio:

Entonces, este no puede ser el camino correcto para resolver una ecuación. – Igualmente, si «cambio de signo» a algo en la ecuación, la balanza pierde su equilibro, porque -5 no es igual a 5. El que «lleva algo al otro lado y cambia su signo», está cometiendo dos graves errores a la vez (cuyos efectos felizmente se anulan).
El principio correcto para transformar y resolver una ecuación, es este:
Toda operación que se efectúa al lado izquierdo de la ecuación, debe efectuarse de igual forma al lado derecho.
Si al lado izquierdo sumo 5, también tengo que sumar 5 al lado derecho. Si el lado izquierdo lo divido entre 3, también tengo que dividir el lado derecho entre 3. Si elevo al cuadrado el lado izquierdo, también tengo que elevar al cuadrado el lado derecho. – Este es el principio correcto que lleva a resultados correctos y no causa confusiones.
(Este principio debe complementarse con el principio de que cada operación matemática se anula por la operación inversa: una suma se anula con una resta y viceversa; una multiplicación con una división, y una potencia con una raíz.)
En nuestro ejemplo del inicio, la aplicación de este principio sería: Restamos 5 a ambos lados de la ecuación.
Claro, la solución final es la misma como con el «procedimiento escolar». Entonces, ¿qué tiene de malo el «llevarlo al otro lado»?
El daño sucede, una vez más, al nivel de los principios. El «procedimiento escolar» es un manejo mecánico sin sentido, que tiene que «hacerse así porque así se hace, y punto.» Si alguien pregunta «¿por qué?», no recibirá explicación, porque matemáticamente este procedimiento no tiene explicación. Como hemos visto, es un procedimiento que contradice los principios matemáticos. Una vez más, el alumno solo aprende una técnica, pero no aprende matemática. Aun peor, aprende principios equivocados: que en una ecuación se pueda «llevar un número al otro lado» y que se pueda «cambiar de signo a un número», sin que esto afecte la veracidad de la ecuación.
Además, el «procedimiento escolar» causa confusión. Tan solamente si avanzamos a ecuaciones con multiplicación o división como estas:
El alumno dirá que en estos casos también hay que «llevar el 5 al otro lado», pero ¿hay que cambiarle el signo o no? ¿No? ¿Por qué no? – Nuevamente, esto no se puede explicar de manera lógica, porque el procedimiento en sí mismo no es lógico. Con esta clase de enseñanza, el alumno tiene que aprender un nuevo procedimiento por separado para cada nueva operación. Cuando llega a potencias y raíces, otra vez tendrá que aprender un procedimiento nuevo (mientras en algún rincón de su cerebro sigue cavilando por qué en la suma había que «cambiar de signo» al 5 y en la multiplicación no.)
Una confusión adicional ocurre en un caso como este:
x / 5 = 13 + a
El alumno «sabe» (o sea, cree equivocadamente) que tiene que «llevar el 5 al otro lado», pero ¿cómo exactamente? ¿Hay que multiplicar el 13 por 5, o la a, o ambos? – El profesor puede decirle que hay que multiplicar ambos, pero ¿por qué? Aquí tampoco hay explicación lógica.
Si nuestro alumno hubiera aprendido el principio correcto desde el principio, no tendría toda esta confusión. (La palabra «principio» por sí misma indica que con esto hay que comenzar: los principios deben ir al principio, no al final.) El principio de la balanza le dice al alumno inequívocamente que puede anular una multiplicación por medio de una división (y es obvio que al dividir, nadie cambia el signo del divisor así por así). A la luz de este principio, también es obvio que al multiplicar la ecuación (ambos lados de la ecuación), hay que multiplicar el contenido completo de los platillos de la balanza, y no solamente una parte. (De otra forma no se mantendría la igualdad.) Además, el principio es general, o sea, se aplica a cualquier operación matemática. El alumno no tiene necesidad de aprender un procedimiento nuevo para cada operación aparte. Así se evitan muchas confusiones cuando se enseña matemática basada en principios, en vez de procedimientos burocráticos.
(Continuará)








