Introducción por el traductor:
¿Sintió usted alguna vez la soledad después de haber reflexionado sobre algún asunto de manera independiente, cuando usted al fin descubrió que llegó a conclusiones completamente diferentes de toda la humanidad alrededor? Así me sentí yo después de escribir la primera versión de mi artículo «Aprender matemática – ¿cuestión de burocracia o de principios?». ¿Será verdad que yo era el único que piensa así, y que el entero sistema escolar está equivocado?
Después descubrí la pequeña obra por Paul Lockhart, «A Mathematician’s Lament» (Lamento de un matemático), y encontré allí el mismo pensamiento fundamental: Lo que en las escuelas se presenta como «matemática», no es en realidad ninguna matemática en absoluto. Así que no soy el único loco en el mundo entero. ¡Qué alivio! Cuánto más, puesto que Paul Lockhart no es «cualquiera»; él es un matemático profesional. O sea, él sabe de qué está hablando.
En algunos detalles no estoy de acuerdo con él. Es obvio que en su trasfondo el tiene una cosmovisión diferente de la mía. Pero las ideas principales de su «Lamento» me parecen buenas, importantes, enriquecedoras, y desafiantes (en un buen sentido). Además, él presenta no solamente críticas, sino también varias ideas constructivas que se pueden aplicar en una escuela alternativa, o aun mejor en la educación en casa. Por tanto, deseo presentar en este blog unos extractos extensos de esta obra, y añadiré mis propios comentarios en algunas partes. El original es un poco largo para un artículo en el blog (25 páginas A4); por tanto me limitaré a las partes más importantes, y dejaré de lado un capítulo entero (acerca del formalismo en las demostraciones geométricas).
Extractos traducidos de «A Mathematician’s Lament», por Paul Lockhart:
La pesadilla de un músico
Un músico se despierta de una pesadilla horrible. En su sueño, él se encuentra en una sociedad que hizo de la música una asignatura escolar obligatoria. «Ayudamos a nuestros alumnos a ser más competitivos en un mundo cada vez más lleno de sonidos.» Pedagogos, sistemas escolares, y el estado, se responsabilizan de este proyecto importante. Se encargan investigaciones, se forman comisiones, y se hacen decisiones – todo sin buscar el consejo o la colaboración de un solo músico o compositor activo.
Puesto que los músicos expresan sus ideas en forma de notas musicales, tenemos que considerar estos extraños puntos y líneas como «el lenguaje de la música». Para que los niños alcancen alguna capacidad musical, necesitan dominar primero este lenguaje. ¿Cómo podríamos esperar que un niño cante una canción o toque un instrumento, sin haber sido educado primero a fondo en la escritura de las notas musicales, y en la teoría de la música? Tocar y escuchar música, son temas muy avanzados que se pueden enseñar solamente en los institutos de educación superior.
La escuela primaria y secundaria, en cambio, son responsables de introducir este lenguaje musical. «En las clases de música usamos nuestro papel de pentagramas y copiamos notas musicales de la pizarra, o las transponemos en una tonalidad diferente. Tenemos que escribir y usar correctamente las claves y los accidentes, y nuestro profesor controla estrictamente que nuestras notas negras estén completamente llenas. Una vez tuvimos un problema difícil acerca de unas escalas cromáticas, y yo lo había resuelto correctamente, pero mi profesor me dio una mala nota porque las plicas señalaban hacia el lado equivocado.»
(…)
En los grados superiores, la presión aumenta más. Para poder entrar a alguna institución de educación superior, los alumnos tienen que dominar la teoría de los ritmos y de las armonías, y el contrapunto. «Es muy exigente; pero cuando por fin llegarán a escuchar música verdadera en su educación superior, valorarán este trabajo de los grados anteriores.» – Por supuesto, serán solamente unos pocos alumnos que se especializarán en música. Por tanto, serán muy pocos que efectivamente llegarán a escuchar los sonidos representados por las notas musicales. «Para decir la verdad, la mayoría de los alumnos no son muy buenos en música. Se aburren en las clases, y sus trabajos escritos apenas se pueden descifrar. Parece que no les interesa la importancia de la música en el mundo actual.» (…)
– El músico se despierta, lleno de sudor. Se siente agradecido al darse cuenta de que todo fue solamente un sueño loco. «¡Claro!», exclama. «Ninguna sociedad reduciría mi arte hermoso y significativo a algo tan aburrido y trivial. Ninguna cultura puede tratar a sus niños de una manera tan cruel, privándolos de tal manera de una expresión natural y recreativa de la creatividad humana. ¡Cuán absurdo!»
(…)
Sin embargo, nuestra enseñanza actual de matemática es una pesadilla exactamente igual a ésta. Si yo tuviera que inventar una estrategia para destruir la curiosidad de un niño, y su amor por inventar patrones, yo no podría encontrar una solución más eficaz que la escuela actual. Yo ni siquiera podría tener ideas tan absurdas y destructoras del alma, como las que dominan la enseñanza actual de la matemática.
Todo el mundo sabe que algo está mal. Los políticos dicen: «Necesitamos exigencias más altas.» – Las escuelas dicen: «Necesitamos más dinero y materiales.» – Los expertos en pedagogía dicen una cosa, y los profesores dicen otra cosa. Pero todos ellos están equivocados. Los únicos que entienden lo que está mal, son aquellos que siempre son castigados y que nadie pregunta por su opinión: los alumnos. Los alumnos dicen: «Las clases de matemática son tontas y aburridas.» Y tienen razón.
Matemática y cultura
En primer lugar tenemos que entender que la matemática es un arte. La única diferencia entre la matemática y otras artes como la música o la pintura, es que nuestra cultura no la reconoce como arte. Todo el mundo comprende que los poetas, los pintores y los músicos crean obras de arte. Nuestra sociedad incluso es bastante generosa con el término «arte»: Arquitectos, chefs, y aun directores de televisión reciben el título de «artistas». Entonces, ¿por qué no los matemáticos?
Una parte del problema es, que nadie sabe realmente lo que hacen los matemáticos. Según la opinión general, parece que de alguna manera están asociados a las ciencias – ¿quizás ayudan a los científicos con sus fórmulas, o alimentan computadoras con números grandes para algún propósito? – La mayoría de la gente piensa que los matemáticos pertenecen a los «pensadores racionales», como opuestos a los «soñadores poéticos».
Pero en realidad no existe nada más soñador, más poético, más radical, más subversivo y más psicodélico que la matemática. La matemática es igualmente abrumadora como la cosmología o la física. (Los matemáticos inventaron «agujeros negros» mucho antes de que los astrónomos realmente los encontraron.) La matemática permite una mayor libertad de expresión que la poesía o la música (puesto que éstas dependen mucho de las propiedades del universo físico). La matemática es el arte más puro; y a la vez el arte más malentendido.
Deseo entonces explicar lo que es la matemática, y lo que hacen los matemáticos. Una descripción excelente es la de G.H.Hardy:
«Un matemática, igual como un pintor o un poeta, es un creador de patrones. Sus patrones son más duraderos que la poesía o la música, porque consisten en ideas.»
O sea, los matemáticos crean patrones que consisten en ideas. ¿Qué clase de ideas? ¿Ideas acerca de los rinocerontes? – No, éstos los dejamos para los biólogos. – ¿Ideas acerca del lenguaje y la cultura? – No, normalmente no. Estas cosas son demasiado complicadas para el gusto de la mayoría de los matemáticos. Si existe algún principio estético general en la matemática, entonces es este: Lo sencillo es lo bello. Los matemáticos prefieren reflexionar acerca de las cosas más sencillas posibles; y las cosas más sencillas posibles son imaginarias.
Nota del traductor: En el caso de que el lector perdió el gozo de la matemática hace mucho tiempo, debido a las clases escolares aburridas, quizás le será difícil comprender lo que dice Lockhart acerca de la matemática como arte, y como un proceso descubridor y creativo. Pero el problema no es con la matemática; el problema es con la escuela. Recomiendo al lector, seguir detenidamente el siguiente ejemplo y reflexionar sobre él, para comprender de qué se trata en el «proceso matemático».
– Yo daría aun un paso más y diría: La matemática, si uno la comprende bien, es una forma de adoración. Consiste en «pensar los pensamientos de Dios detrás de El» (como dijo Juan Kepler). Esto es lo que sintieron los grandes científicos del pasado como Newton, Kepler o Maxwell, frente a las leyes matemáticas que rigen el universo. Ellos vieron en la matemática un reflejo de los «decretos de Dios» que gobiernan y mantienen el mundo.
Por ejemplo, si me da ganas de pensar acerca de unas formas geométricas – esto sucede a menudo -, entonces yo podría imaginarme un triángulo en una caja rectangular:

Me pregunto, ¿qué parte de la caja ocupa este triángulo? – ¿Quizás dos tercios?
Ahora es importante entender que no estoy hablando acerca de este dibujo de un triángulo en una caja. Tampoco estoy hablando de un triángulo de metal que es parte de la estructura de un puente. No tengo ningún propósito práctico. Simplemente estoy jugando. Esto es matemática: Tener curiosidad, jugar, dialogar con mis propias imaginaciones.
La pregunta, ¿cuál parte de la caja ocupa el triángulo?, por ahora ni siquiera tiene sentido, en relación con verdaderos objetos físicos. Aun el triángulo material hecho de la manera más precisa, es todavía una colección desesperadamente complicada de átomos oscilantes, que constantemente cambian su forma. Excepto si queremos hablar solamente acerca de unas medidas aproximadas. Pero esto nos lleva a toda clase de detalles del mundo real. Eso lo dejamos para los científicos. La pregunta matemática trata de un triángulo imaginario en una caja imaginaria. Sus lados son perfectos, porque yo quiero que sean así. Este es un tema importante en la matemática: Las cosas son tales como usted las quiere. Usted puede escoger entre alternativas interminables; el mundo real no va a interferir con nada.
Pero una vez que usted ha hecho sus decisiones (por ejemplo, si su triángulo será simétrico o no), entonces sus creaciones harán lo que tienen que hacer por sí mismas, lo quiera usted o no. Esto es lo sorprendente de los patrones imaginarios: ¡ellos le dan respuestas! El triángulo ocupa una parte determinada de la caja, y yo no puedo decidir cuánto es esta parte. Es un número exactamente determinado, y yo tengo que decubrir cuánto es.
O sea, comenzamos a jugar y a imaginarnos lo que queremos, y formamos patrones y hacemos preguntas acerca de ellos. Pero ¿cómo encontramos las respuestas a las preguntas? Esto no es como en las ciencias. No puedo hacer ningún experimento con tubos de ensayo o con máquinas, para descubrir la verdad acerca de una figura que yo mismo he imaginado. Las preguntas acerca de nuestras imaginaciones pueden responderse solamente mediante nuestras imaginaciones, y esto es un trabajo duro.
En el ejemplo del triángulo, yo veo algo sencillo y bonito:
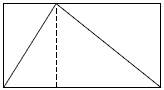
Si yo corto el rectángulo de esta manera en dos rectángulos, entonces puedo ver que cada parte a su vez es partida diagonalmente en dos mitades por uno de los lados del triángulo. O sea, dentro del triángulo existe la misma cantidad de espacio como afuera del triángulo. Esto significa que ¡el triángulo ocupa exactamente la mitad de la caja!
Así se ve y se siente un pedazo de matemática. El arte del matemático consiste en hacer preguntas sencillas y elegantes acerca de nuestras criaturas imaginarias, y en encontrar explicaciones satisfactorias y hermosas. Este ámbito de las puras ideas es fascinante, divertido, ¡y no cuesta nada!
¿De dónde vino esta idea mía? ¿Cómo se me ocurrió dibujar esta línea adicional? ¿Cómo sabe un pintor adonde debe apuntar con su pincel? – Inspiración, experiencia, intentos y errores, o simplemente la suerte. Esto es todo el arte; un arte que transforma cosas en otras cosas. La relación entre el rectángulo y el triángulo era un secreto, y entonces una pequeña línea lo reveló. Primero no pude verlo, y de repente lo vi. De alguna manera pude crear desde la nada una belleza profunda y sencilla, y yo mismo fui cambiado en el proceso. ¿No es esta la esencia de todo arte?
Por eso se me quebranta el corazón cuando veo como se trata la matemática en las escuelas. Esta aventura rica y fascinante de la imaginación se reduce a una colección de «datos» estériles para memorizar; y procedimientos que se deben aplicar. Los alumnos nunca reciben la oportunidad de hacer esta pregunta sencilla y natural acerca de las figuras; y tampoco se les permite pasar por este proceso creativo y enriquecedor de inventar y descubrir. En lugar de ello, son confrontados con lo siguiente:

Fórmula del área del triángulo: A = 1/2 b h
«El área de un triángulo es igual a la mitad del producto de su base con su altura.» – Los alumnos tienen que memorizar esta fórmula y después «aplicarla» en incontables ejercicios. Toda expectativa y todo gozo se esfuma, y también desaparece el esfuerzo y la frustración del proceso creativo. Aquí ni siquiera existe un problema. La pregunta fue respondida apenas que fue hecha – al alumno ya no le queda nada por hacer.
Deseo clarificar qué es lo que estoy criticando. No estoy en contra de las fórmulas, ni en contra del aprender hechos interesantes. Todo eso está bien en su contexto apropiado, y tiene su lugar, igual como el aprender palabras es necesario para aprender un idioma extranjero. Estos conocimientos ayudan a crear obras de arte más ricas y más detalladas. Pero lo esencial no es el hecho de que el triángulo ocupa la mitad de la caja. Lo esencial es la hermosa idea de dividirlo por medio de esta línea. Esto puede inspirar otras ideas hermosas, y puede llevar a descubrimientos creativos en otros problemas. Una mera exposición del hecho no puede proveer esta inspiración.
Si dejamos de un lado el proceso creativo, y dejamos solamente su resultado, entonces nadie se sentirá involucrado en ello. Es como si alguien me dice que Miguel Angel creó una escultura hermosa, pero no me permite ver la escultura. ¿Cómo me podría inspirar eso? (En realidad, es aun peor. Si alguien habla de Miguel Angel, por lo menos entiendo que existe el arte de la escultura, y que no se me permite admirarla.)
La matemática escolar se fija solamente en el «¿Qué?», y pasa por alto el «¿Por qué?». Así se reduce la matemática a una cáscara vacía. El arte no está en la «verdad»; el arte está en la explicación de la verdad, en la argumentación. (…) La matemática es el arte de explicar. La escuela quita a los alumnos la oportunidad de participar en este arte: de plantear sus propios problemas, de hacer sus propias hipótesis y descubrimientos, de equivocarse, de experimentar una frustración creativa, de tener una inspiración, y de armar sus propias explicaciones y demostraciones. Por eso, la escuela les quita la misma matemática.
Entonces, no me quejo de que las clases de matemática contengan hechos y fórmulas. Me quejo de que la misma matemática está ausente en nuestras clases de matemática.
(…)
Muchos profesores de matemática transmiten la idea (explícitamente o con su ejemplo) de que la matemática trata de memorizar fórmulas y definiciones y algoritmos. ¿Quién corregirá esta idea equivocada?
Este problema cultural es un monstruo que sigue procreándose: Los alumnos aprenden de sus profesores lo que (supuestamente) es la matemática, y éstos a su vez lo aprendieron de sus profesores, y así se repite en cada generación esta falta de comprensión y valoración de la matemática. Aun peor: Esta «seudo-matemática», este énfasis en la manipulación correcta (pero sin sentido) de símbolos, crea su propia cultura y sus propios valores (equivocados). Aquellos que la dominan, se vuelven presumidos. No quieren saber nada de que la matemática es creatividad y estética. A muchos alumnos, sus profesores les dijeron durante diez años que eran «buenos en matemática»; pero cuando llegaron a la universidad, se decepcionaron al descubrir que no tenían ningún talento matemático. Solamente habían sido «buenos» en seguir las órdenes de otras personas. Pero la matemática no trata de seguir las órdenes de otra gente. Se trata de descubrir direcciones nuevas.
(…)
Nota del traductor: Lockhart menciona aquí un problema importante; uno que he examinado desde una perspectiva un poco diferente en «Aprender matemática – ¿cuestión de burocracia o de principios?»: El sistema escolar entrena a los alumnos a funcionar mecánicamente como calculadoras; pero no se les enseña verdaderos principios matemáticos. Entonces el alumno piensa que la matemática consiste en seguir ciegamente las órdenes del profesor – órdenes que a menudo son incomprensibles o no tienen sentido. Se enseña solamente el «¿Qué?», pero no el «¿Por qué?». Nunca se dice al alumno que las leyes matemáticas son un «bien común», que están en el «dominio público», y que él mismo puede descubrirlas.
La continuación profundizará el tema de la matemática en las escuelas.
(Continuará)





