En artículos anteriores describí algunas formas como los niños pueden aprender matemática en los quehaceres cotidianos del hogar, en sus juegos, y en sus pasatiempos. Describiré ahora un proyecto que mantuvo el interés de uno de nuestros hijos durante un tiempo prolongado (más que un año) y le incentivó a aprender muchos conceptos de geometría.
Cómo nació este proyecto
Deseamos dar a nuestros hijos la oportunidad de aprender según sus propios intereses. Este proyecto puede ser interesante para niños a quienes les gusta hacer trabajos manuales con papel y cartulina, y construir diversos objetos. Este fue el caso de nuestros hijos. Entonces, como padres no hemos comenzado diciendo: «Esta sería una forma novedosa de aprender geometría, vamos a hacer eso con nuestros hijos.» Al contrario, el interés de los niños fue lo primero. Observamos que ellos pasaban horas armando modelos recortables de cartulina prediseñados: casas y carros sencillos, animalitos, y con el tiempo también construcciones más complicadas. Se pueden encontrar diversos modelos ya prediseñados en internet para descargar, desde sencillos hasta muy complicados. La «fiebre de los recortables» contagió también a algunos amigos de nuestros hijos. Pero en algún momento esos modelos prediseñados ya no eran tan interesantes para los niños; entonces el siguiente desafío fue construir sus propios modelos. Convertimos este interés en un proyecto educativo. Para construir modelos propios, es necesario aprender diversas construcciones geométricas con regla, escuadra y compás. Y esta experiencia a su vez ayuda a los niños a entender los conceptos de la geometría. Para los niños, el mejor camino de aprendizaje comienza siempre con la experiencia concreta y práctica, y de allí procede hacia las generalizaciones y los conceptos abstractos.
Otros niños pueden tener otros intereses que los motivan a aprender matemática y geometría: cocinar según recetas; orientarse con mapa y brújula; tejer; carpintería; gráficos computarizados; etc. Todas estas actividades tienen mucha relación con la matemática y pueden servir como «puerta de entrada» hacia un proyecto interesante. Encuentre algo que capte el interés de sus hijos.
Prerrequisitos para este proyecto:
Como mínimo, los niños deberían entender unos conceptos básicos de la geometría: lo que es un ángulo; lo que significa «paralelo»; y los nombres de las figuras geométricas. En el caso que no lo sepan, habría que introducir estos conceptos durante los primeros trabajos prácticos. – Además, los niños deberían tener un poco de práctica en medir y marcar segmentos rectos con una regla.
Introducción para los niños:
El trabajo más sencillo para principiantes es fabricar una caja rectangular. Como introducción, podemos conseguir unas cajas de crema dental, de filtrantes de té, de jaboncillos, medicamentos, o parecido. Abrimos una o varias cajas para ver cómo son hechas. No hay que cortarlas al abrir; hay que separar cuidadosamente las partes pegadas. Así aparece la forma original (plana) de la caja, y los niños pueden ver como esta forma resulta en una caja, doblando y pegándola. Una vez que han entendido el principio, pueden construir su propia caja con las medidas que ellos mismos eligen. Seguramente se darán cuenta de que existen diversas posibilidades de diseñar la caja: adhiriendo todas las paredes laterales al fondo, o juntando las paredes laterales entre sí; etc.
La única construcción geométrica necesaria para este modelo es el rectángulo. Además, los niños tienen que entrenar su capacidad de imaginarse el objeto tridimensional, para entender dónde tienen que colocar lengüetas para poner goma, y cómo armar el modelo final. – Como regla, es mejor diseñar demasiadas lengüetas que muy pocas. Si al armar el modelo se nota que una lengüeta no es necesaria, se puede cortarla fácilmente; pero es más trabajo aumentar una lengüeta adicional si nos damos cuenta de que falta una.
Dificultades al construir rectángulos:
Los niños tendrán que acostumbrarse a dibujar tanto las rectas como los ángulos según la medida correcta. Muchos niños medirán al inicio solamente los lados del rectángulo, pero dibujarán el ángulo recto como les parece, sin medirlo. Entonces, si miden los nuevos lados y unen sus extremos para dibujar el último lado, probablemente notarán que este último lado no tiene la longitud correcta. – Si no lo notan, hay que señalárselo. O podemos esperar hasta que estén pegando la caja, y entonces notarán que la caja sale chueca.
Los niños tienen que aprender entonces cómo construir un ángulo recto, usando la escuadra.
Proyectos para principiantes
Estas son algunas otras construcciones bastante fáciles:
Casa con techo en caballete:
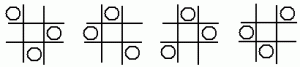
La pared lateral de la casa es un rectángulo con un triángulo encima. Después de construir una de estas paredes, la pared opuesta debe construirse congruente a la primera. Pero para principiantes puede ser demasiado difícil, construir una figura congruente a una figura dada. Es preferible enseñarles que dibujen el triángulo superior de una de las siguientes maneras:
a) midiendo la base (= el lado superior del rectángulo) y los ángulos adyacentes, usando el transportador.
b) midiendo la base y la altura, trazando la altura desde el punto medio de la base.
Alumnos un poco más avanzados pueden en este punto también aprender la construcción de un triángulo a partir de las longitudes de sus tres lados (con compás). Además se pueden tratar en este contexto las leyes de congruencia en los triángulos.
Para construir las dos partes del techo correctamente, hay que medir su lado lateral en el triángulo ya dibujado. Si los niños no se dan cuenta de eso por sí mismos, habrá que enseñárselo.
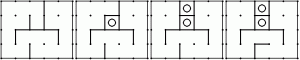
Así podría verse el recortable para construir esta casa.
Si queremos que el techo sobresalga por los lados, tenemos que construirlo como una pieza aparte y hacerlo un poco más grande que la casa:
Otras casas:
Se pueden diseñar las variaciones más diversas de casas. Unos ejemplos:
– Una casa con techo en caballete, donde el caballete no se encuentra en el medio (o sea, una parte del techo es más larga que la otra). En este caso es importante dibujar la pared opuesta de la casa en forma reflejada.
– Una casa con dos alas en ángulo recto. Con techo plano, esta construcción es bastante fácil. Pero este tipo de casa con caballete (o sea, dos caballetes en ángulo recto) ya es bastante difícil; la mayoría de los niños no podrán construirlo sin ayuda. La solución más fácil consiste en construir primero un plano de la casa; de allí podemos medir las longitudes de los caballetes hasta su intersección. Las otras medidas dependen de las medidas de las paredes.
Si el caballete se encuentra en el medio, entonces podemos también demostrar que su longitud es igual al promedio de las longitudes de las dos paredes paralelas a él. (Geométricamente, es la línea media de un trapecio.) Entramos aquí al tema de las figuras semejantes, las proporciones, y teoremas relacionados.
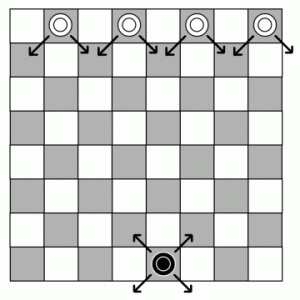
Esta es una posibilidad de construir un recortable para la casa arriba mostrada.
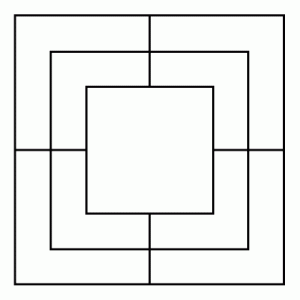
– Una torre con techo en forma de pirámide. Esto es más fácil si la base de la torre es un cuadrado. En este caso, el techo consiste en cuatro triángulos congruentes.
Un carro sencillo:
Este modelo sencillo consiste solamente en dos lados iguales (o sea, reflejados), y el techo de en medio. Por abajo queda abierto. Para construir un modelo de este tipo hay que comenzar con uno de los lados, y delimitarlo enteramente con líneas rectas (con excepción de las ruedas). Con principiantes se recomienda todavía no usar formas redondas. (De los participantes en nuestros programas vacacionales, solamente los alumnos más avanzados lograron construir un cilindro como su primera forma redonda, y eso recién en la doceava lección.) – Aquellos niños que todavía no saben usar un compás, usarán un objeto redondo (p.ej. una moneda) para dibujar las ruedas.
Después de terminar un lado del carro, construimos sobre su lado superior una tira recta que formará el techo del carro. Los dos lados de esta tira tienen que ser paralelos.
Dividimos esta tira en rectángulos, de manera que la longitud de cada rectángulo corresponde a la longitud de uno de los segmentos del lado del carro.
Finalmente construimos al lado opuesto de la tira el otro lado del carro, congruente (pero reflejado) al lado que construimos al inicio. Aquí surgirá nuevamente el problema de que muchos niños medirán solamente las longitudes de los segmentos, pero dibujarán los ángulos sin medirlos con exactitud. Es bueno primero dejarlos que lo hagan así, y después comprobar la congruencia. Hay diversas maneras de realizar esta comprobación: Uno puede medir los ángulos y/o las diagonales; o se puede terminar de armar el primer modelo, y entonces se notará que sale chueco si los dos lados no son congruentes. También se puede doblar la cartulina de tal manera que los dos lados del carro se sobreponen, y mirarla hacia una luz fuerte. Si las líneas son suficientemente nítidas, se pueden ver los dos lados uno sobre el otro, y así se puede ver fácilmente si son congruentes o no. Así los niños llegarán a entender que en los polígonos con más de tres lados no es suficiente que tengan lados iguales para que sean congruentes, sino que también los ángulos tienen que ser iguales.
Proyectos propios
Después de dominar las construcciones sencillas como las que acabamos de describir, los niños podrán inventar y construir otros modelos con líneas rectas: otras variaciones de casas; muebles como mesas, sillas, etc; cuerpos geométricos; un tren; etc. A menudo los niños tienen ideas interesantes y novedosas. Por ejemplo, una alumna fabricó un modelo de un lápiz. – Es claro que a veces necesitan ayuda para sus construcciones. Así practicarán y aprenderán nuevos conceptos geométricos.
(Continuará)
 |
Vea también:Libros de Matemática Activa
para un aprendizaje sistemático según los principios expuestos en este artículo. |
